日前,北京理工大学物理学院张向东教授课题组和信息与电子学院孙厚军教授课题组合作,在拓扑电路和高阶拓扑态研究方面取得重要进展。相关系列研究成果发表在近期的Phys.Rev.Lett.以及Phys.Rev.BRapidCommunications(Editor’sSuggestions)上,系列研究工作得到了国家自然科学基金委和国家重点研发计划的资助。
探究固体材料和经典波系统的拓扑性质是近几年研究的热点。基于体边缘对应定理,大多数N维拓扑系统都支持N-1维的边界态。最近,一类由对称性保护的高阶拓扑绝缘体被提出,它们支持更低维度的拓扑边缘态并且遵从更一般化的体边缘对应定理[Science357,61(2017)]。自2017年高阶拓扑态的理论方案被提出后,在量子材料和经典人工系统中观察高阶拓扑相的报道陆续出现。然而由于众多实验上的限制,起初的工作都只局限于二维周期系统中的高阶拓扑相,包括体四极子以及边界偶极子诱导的零维角态。实现三维甚至更高维度的高阶拓扑物态以及在无序系统中探索高阶拓扑相的存在具有一定的挑战性。
基于凝聚态物理系统中晶格与电子线路网络的一致性,通过设计经典电路可以模拟凝聚态体系中新奇的微观效应。相比于固体材料和一些其它的经典系统(如电磁波和声波系统等),经典线性电路具有灵活可重构的连接特性。同时,线性电路的性质是由电路网络中端点连接的方式决定的,与线路的具体形状和空间维度无关。因此,一些在凝聚态系统以及其它经典系统中很难实现的量子物态,有望在电路系统中被实现。近期,来自北京理工大学的研究团队,利用经典电路平台率先实现了三维八极拓扑相,四维高阶拓扑相以及由无序引起的高阶安德森拓扑相。
1.基于经典电路的三维八极拓扑相
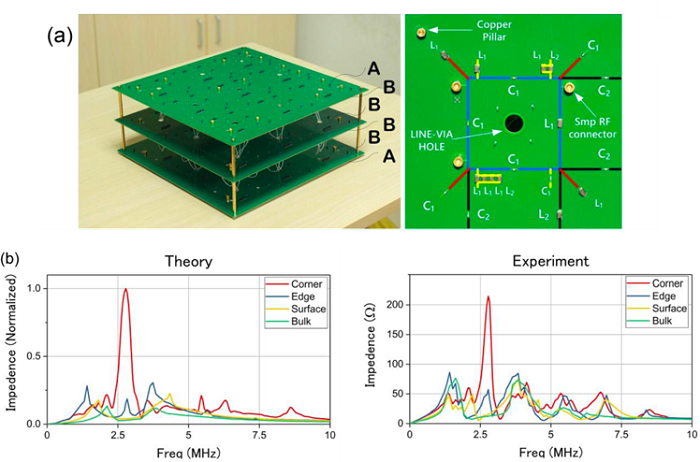
图1.(a).三维八极子电路样品图。(b).三维八极子电路理论模拟和实验测量结果。
通过构造x,y,z三个方向的非互易反演对称性,由体八极子诱导的三维八极拓扑相可以产生,该三维八极拓扑相支持拓扑保护的零维角态。实现三维八极拓扑相的经典类比需要在实空间构造正和负的格点耦合,该苛刻的要求很容易通过电路网格节点间电容和电感的连接来实现。进而,通过设计三维电路节点的连接和接地,由基尔霍夫方程导出的电路导纳矩阵具有和支持体八极子紧束缚哈密顿量相同的形式。因此,所设计的经典电路可以展现八极子拓扑绝缘体的新奇性质。图1a显示了加工的电路样品图和其局域放大图。通过测量电路角落节点的阻抗响应,能隙中的高阶拓扑角态可以被验证。理论模拟和实验测量结果显示在图1b中。

2019年11月,相关工作在Phys.Rev.B上以RapidCommunications的形式发表[Phys.Rev.B,100201406(R)(2019)]。北京理工大学信息与电子学院博士生包嘉诚和物理学院博士生邹德源为论文的共同第一作者。值得指出的是,在上述工作发表后,八极子拓扑绝缘体进一步在声学[Nat.Commun.112108(2020),Nat.Commun.112442(2020)]和电路系统[Light:Science&applications9145(2020)]中进一步得到了验证。
2.基于经典电路的四维十六极拓扑相
高维空间的拓扑物态通常具有众多新奇的物理性质。然而,由于三维空间的限制,天然存在的量子材料和人工设计的经典结构都难以实现高于三维空间的拓扑物态。人造维度为人们在实验上实现高维拓扑态提供了重要的途径,但是目前的技术仍然具有一定的局限性,使得对很多高维拓扑物态的研究仍然停留在理论层面。因此,寻找能够构造高维拓扑物态的新型平台具有重要的意义。
经典电路的性质是由电路网络中端点的连接方式决定的,与线路网络的具体形状和空间维度无关。因此,高维空间的电路网络可以被投影到二维平面。通过在二维平面设计原始高维电路网络的节点连接,可以在等效的二维电路网络中实现高维电路的新奇效应。

图2.(a)和(b)四维十六极子电路理论模型和实验样品图。(c).拓扑及平庸电路的阻抗测量结果。(d).不同缺陷对四维十六极高阶角态的影响。
基于这一优势,研究者设计了由四维非互易反演对称性保护的十六极拓扑绝缘体的经典电路类比。理论模型和样品结构分别显示在图2a和2b中。通过对拓扑和平庸电路进行对比数值模拟和实验测量,四维十六极子诱导的零维角态被验证,相应的实验结果显示在图2c中。另外,申请者也对不同形式的缺陷对高维高阶拓扑态的影响进行了研究,发现只有特殊节点的缺陷会显著影响高阶角态的能谱特性,相关实验结果显示在图2d中。

相关工作在Phys.Rev.B上以RapidCommunications的形式发表[Phys.Rev.B,100201406(R)(2019)]。该工作受到了编辑的高度评价,被选为Editors’suggestions。北京理工大学物理学院2015级博士生张蔚暄(现为信息与电子学院特立博士后)和物理学院博士生邹德源为论文的共同第一作者。
3.基于经典电路的高阶安德森拓扑相
一般来说,强的无序效应会使拓扑系统的能隙闭合,从而破坏拓扑相的存在。与该传统的认识不同,2009年,来自香港大学的沈顺清课题组理论证明无序可以诱导拓扑态的形成[Phys.Rev.Lett.102,136806(2009)],并为其取名为安德森拓扑绝缘体。随后,众多课题组利用不同的系统对安德森拓扑绝缘体进行了实验验证。近期,随着对高阶拓扑绝缘体研究的深入,一个重要的问题是:高阶安德森拓扑绝缘体是否存在;如果存在,如何对其进行实验验证。
近日,来自北京理工大学的研究团队基于修正的Haldane模型(引入附加的晶格形变),通过引入次近邻耦合相位的无序效应,证明了高阶安德森拓扑相的存在。相应的理论模型和计算结果显示在图3a中。从数值计算结果可以清晰的看到,随着次近邻耦合相位无序程度的增大,系统能隙会打开,并伴随拓扑态的产生,绿色区域标记了零维角态存在的区域。另外,系统在该区域具有量子化的分数电荷,进一步证明了无序引起的高阶拓扑效应。
上述晶格模型具有复杂的格点耦合,利用光、声等人工结构构造其经典类比具有非常大的难度。为了解决这一问题,研究者结合‘编织’与‘非编织’的电路网络节点耦合,分别实现了有效的次近邻和最近邻格点耦合。利用大小不同的耦合器件,构造了有效的晶格形变。所设计的样品图显示在图3b中。进一步,研究者通过控制无序‘编织’连接的电路网路节点比例,对所设计的电路系统引入不同强度的次紧邻耦合无序。随着无序强度的增加,研究者观察到了无序引起的零维角态,证明了高阶安德森拓扑相的存在。相应的实验结果显示在图3c中。
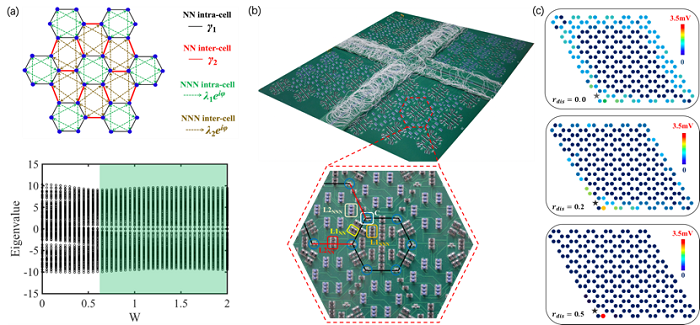
图3.(a)理论模型和计算结果;(b)安德森电路实验样品图;(c)次紧邻耦合相位引起的零维角态实验测量结果。
相关工作在Phys.Rev.Lett.上发表[Phys.Rev.Lett.,126146802(2021)]。北京理工大学物理学院2015级博士生张蔚暄(现为信息与电子学院特立博士后)和博士生邹德源为论文的共同第一作者。值得指出的是,近期两篇相关的理论工作[Phys.Rev.Lett.125166801(2020);Phys.Rev.B103085408(2021)]同样证明了无序引起的高阶拓扑相的存在。







